
Thank you very much for all the work you do on your website, I have found the information you provide extremely helpful. 05).įor Example 1, the output from =BCORREL(B4:B24,A4:A24,TRUE) is shown in range T4:T8 of Figure 2. If lab = TRUE then an extra column of labels is appended to the output (default FALSE) and alpha = the significance level (default. R1 is assumed to contain only 0’s and 1’s. Here R1 and R2 are numeric column arrays with the same number of rows. Real Statistics Function: BCORREL is actually an array function as follows:īCORREL(R1, R2, lab, alpha) = a column array with the following five values: the biserial correlation coefficient for the data in R1 and R2, z-statistic, p-value and left and right limits of the 1– alpha confidence interval. 410).įigure 2 – Confidence interval for biserial correlation We also see that the confidence interval for ρ b is (-.525. 78, we conclude that ρ b is not significantly different from zero. įor Example 1, z = -.27, as calculated in cell O7 of Figure 2. Multiplying these limits by √5/2 produces confidence interval limits for ρ b. Taking the Fisher inverse of these confidence interval limits yields the limits of a confidence interval for 2 ρ b /√5. The 1– α confidence interval for (2 ρ b/√5)′ is We can use z to test whether ρ bis significantly different from zero based on the two-tailed p-value = 2*NORM.S.DIST(-ABS(z), TRUE). Here, x′ = FISHER( x) and the denominator is the standard error. Observation: The following statistic is standard normally distributed The biserial correlation coefficient for Example 1 can be calculated using the BCORREL function, as shown in cell G6 of Figure 1. Real Statistics Function: The following function is provided in the Real Statistics Resource Pack.īCORREL(R1, R2) = the biserial correlation coefficient corresponding to the data in column ranges R1 and R2, where R1 is assumed to contain only 0’s and 1’s.

Note that the value is a little more negative than the point-biserial correlation (cell E4). The biserial correlation of -.06968 (cell J14) is calculated as shown in column L. The biserial correlation coefficient can also be computed from the point-biserial correlation coefficient using the following formulaĮxample 1: Calculate the biserial correlation coefficient for the data in columns A and B of Figure 1.įigure 1 – Biserial Correlation Coefficient
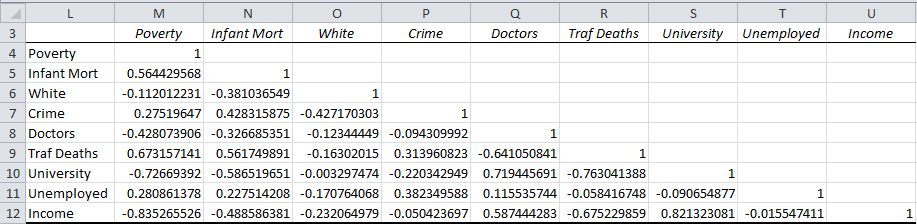
The biserial correlation coefficient provides a better estimate in this case.Īssuming that we have two sets X =, s is the population standard deviation of Y and In such cases, the point-biserial correlation generally under-reports the true value of the association. The biserial correlation coefficient is also a correlation coefficient where one of the samples is measured as dichotomous, but where that sample is really normally distributed. In Relationship between Correlation and t Test and Relationship between Correlation and Chi-square Test we introduced the point-biserial correlation coefficient, which is simply the Pearson’s correlation coefficient when one of the samples is dichotomous.


 0 kommentar(er)
0 kommentar(er)
